Research by Vladimir Zelevinsky
Level Density
By Vladimir Zelevinsky
In a bound many-body quantum system, the energy spectrum of stationary states is discrete. However, with energy growing, the spacings between the levels typically become smaller. In all experiments where the energy resolution is finite, it is usually impossible to speak about exact individual states above certain excitation energy. The only possible formulation is then statistical so that we have to introduce the concept of level density, the number of levels within some energy interval. This idea is especially important at low excitation energy in the continuum, above the threshold of bound states. Not too far from the threshold, the states are still quasitationary, which means that they live a relatively long time: projectile is captured by the nucleus and this compound system decays back after time much longer than the time of flight of a projectile through the system.
Therefore the knowledge of the level density is absolutely necessary for the evaluation of the probability of various reaction channels, both in the laboratory and for astrophysical reactions in the stellar environment. Traditionally the main ways for calculating the level density were either pure phenomenology, for example assuming the nucleus as a gas of fermions at some temperature, or by combinatorics that counts number of ways these fermions can be distributed by their orbitals.
Currently, due to the development of ideas of quantum chaos and due to the great computational opportunities, we can practically exactly calculate the level density in the restricted orbital space. The stationary states of a many-body quantum system of interacting particles become exceedingly complicated with the growth of energy. We cannot solve the quantum equations exactly, but those states are close to the limit of quantum chaos that has its own statistical regularities. Instead of solving many-body Schroedinger equation in a space of billion-like dimension we just make the statistical treatment taking into account the properties of the Hamiltonian of the system for various distribution of particles over orbitals. This can be done including all available interactions, for a given set of exact quantum numbers of the system (angular momentum, parity and isospin). In the space of several neutron and proton shells we also have a special treatment excluding the spurious states corresponding to the motion of the nucleus as a whole.
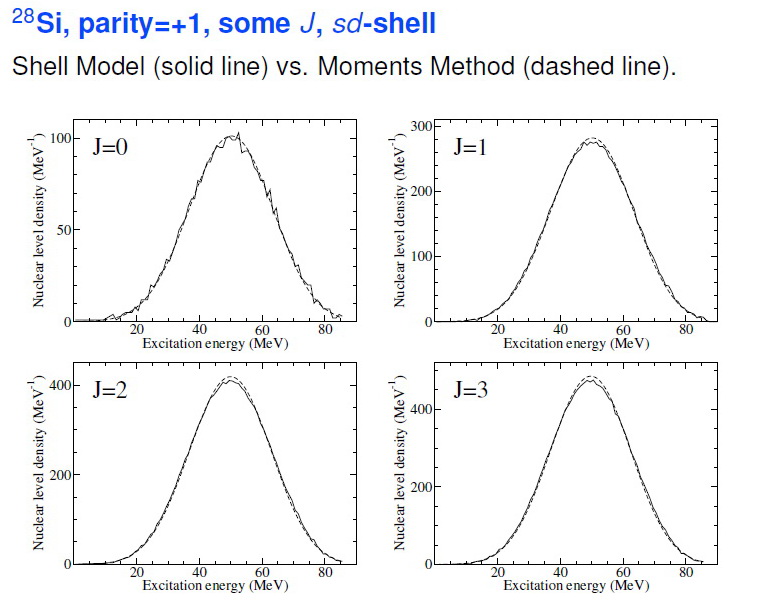
In cases when the model space is not too large the exact solution is possible (as in the sd shell basis) and we can check our statistical method. Excellent agreement is obtained as seen in the figure - the slightly jagged solid line is the density obtained from the exact shell model calculations. The smooth dashed line (often on top of the solid line) is obtained with our statistical method. In cases of a larger model spaces, the exact calculation cannot be carried out, but our methods can be used. This is important for reactions that go to final states at high excitation energy, such as the (n,gamma) reaction of importance for nuclear astrophysics. From a theoretical viewpoint one important conclusion is that the correct account for all types of interactions is very important smoothing the level density compared to pure combinatorics.
References
[1] R.A. Sen'kov, M. Horoi, and V.G. Zelevinsky, High-performance algorithm for calculating non-spurious spin- and parity-dependent nuclear level densities, Phys. Lett. B 702, 413 (2011). [link to paper].
[2] R.A. Sen'kov, M. Horoi, and V.G. Zelevinsky, A high-performance Fortran code to calculate spin- and parity-dependent nuclear level densities, Computer Physics Communications 184, 215 (2013). [link to paper].
[3] R.A. Sen'kov, V.G. Zelevinsky, and M. Horoi, Statistical approach to nuclear level density, AIP Conference Proceedings 1619, 152 (2014). [link to paper].



